Brakes – Numerical Analysis Preview
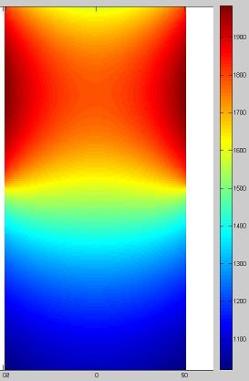
I threw together a Matlab code to simulate the brakes I wrote about. It is currently modeled too simply to bother releasing articles.
Here is a list of assumptions I will work on eliminating.
- Steady State
- Flat Plate 1m Deep
- Constant h (Convection Coefficient)
- Constant k (Thermal Conductivity)
- Constant epsilon (Emissivity)
- No heat into brake pads
- Pads never block heat escape from rotors
- No surface slots
- No venting holes
- Constant properties
- Corners treated simply (no effect on convection/radiation)
- 100% Kinetic Energy loss becomes Heat applied to Rotor
The idea is I will release code, and theory behind it. When I add new articles generally it will be with corrections or new results after eliminated assumptions. For example, the Thermal Conductivity of Carbon changes with temperature, but it is treated as constant at the moment. If I tried to make the numerical solver in one try it would be a mess beyond my patience. If you would like to see what I have now, as far as code, equations, pictures I drew to help visualize what I’m doing, send me a comment. FYI I realized why my temperatures are so high. I accidently (mathematically) assumed that one rotor was absorbing the energy of the car. I’m too lazy to update the picture above for this preview, but the change will certainly reduce the maximum temperature. I quick ran the simulation again and the max temperature went down to 1165Kelvin from 1985Kelvin. The picture above is out of date. Comment if you want to know more before the next release.

Meter thick brake rotors are a bit on the heavy side
Indeed they are. That’s why I listed them as a simplifying assumption. I didn’t make that assumption thinking it was a good one. I did it to simplify the code in the very initial stages to make sure it was working. I am not an industry expert but one of the first things I do, and I think most professionals do, is get initial results that are simplified and normalized. For example, assuming 1 unit length depth, or one second, or whatever the case, before eliminating that assumption to complete the problem. In applied calculus I do this all the time. You can take the Integral for example, make sure it’s correct, then apply the constants outside the integral. It keeps things cleaner and clearer.
In reality the I will have to eliminate the rectangular assumption, which through that alone will erase the 1m depth “placeholder” I have started with. It will make for a more accurate analysis, and lighter brakes 🙂
Thanks for the comment.