Skip to content
Tags

, , , , , , , , , ,

Couette-Poiseuille Combination Take 2

November 21, 2011

There will be an update to this article in the near future at www.consultkeithyoung.com/tags/aerodynamics.

The Navier-Stokes equations in Cartesian Coordinates are:

\rho (\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z}) = -\frac{\partial P}{\partial x} + \mu (\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}) + \rho g

\rho (\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z}) = -\frac{\partial P}{\partial y} + \mu (\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2}) + \rho g

\rho (\frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z}) = -\frac{\partial P}{\partial z} + \mu (\frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2}) + \rho g

Very few physical conditions exist which Navier-Stokes can be solved for analytically. Even with many simplifying assumptions made the solutions can be generally so ugly that the only method for solution is numerical iteration.

Lets make some assumptions. First, assume the air is Fully Developed. This means the air will not be accelerating in the X direction. Obviously in the real world, toward the start of the underfloor this would not be the case, as with all other assumptions I will make. Another assumption is the problem is Steady State. The only velocity is in the X direction and it only accelerates with respect to the Y direction. The pressure only changes with respect to the X direction.

Navier Stokes Assumptions

This leaves us with the very manageable:

0 = -\frac{\partial P}{\partial x} + \mu \frac{\partial^2 u}{\partial y^2}

\frac{\partial^2 u}{\partial y^2} = \frac{1}{\mu} \frac{\partial P}{\partial x} = \lambda = {Constant}

\iint \frac{\partial^2 u}{\partial y^2} = u(y) = \frac{1}{2} \lambda y^2 + A y + B

Assume No Slip

V = \frac{1}{2} \lambda (h)^2 + A (h) + B

0 = \frac{1}{2} \lambda (-h)^2 + A (-h) + B

B = \frac{V-\lambda h^2}{2} = \frac{\mu V - \frac{d{P}}{d{x}} h^2}{2 \mu}

A = \frac{V}{2 h}

u(y)=\frac{1}{2} [\frac{1}{\mu} \frac{dP}{dx}] y^{2} + \frac{V}{2h} y + \frac{\mu V - \frac{dP}{dx} h^{2}}{2\mu}

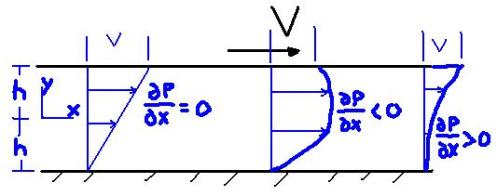
When this is tested by putting in the h value (half of the ride height with the correct sign) and the boundary condition velocity (car velocity for the body or zero for the floor) it is seen that regardless of the Pressure Gradient, the Boundary Conditions agree with the No Slip assumption.

Also it can be seen that if the Pressure Gradient is negative, meaning the pressure is lower at the back than the front, then the air is sucked through and the velocity profile agrees. Conversely if the pressure increases as the flow travels down the floor of the car, the flow is resisted.

This is obviously based on may assumptions that are not true in racing. Air will flow in under the sidepods, turbulence effects will take place, I could go on. What this does do however is show why sucking the air through the underbody is essential to increasing the velocity of the airflow under the car in order to reduce pressure.

I plan on making a Matlab code to simulate this. If anyone can find a similar physical experiment please let me know so I can compare my results.

From → Aerodynamics, Ground Effect, Math, Technical

One Comment

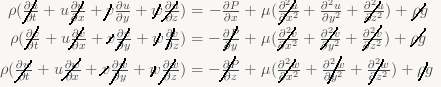
Trackbacks & Pingbacks

  1. Couette-Poiseuille Combination Take 1 « racingtech

Leave a comment

«
»